服务类六西格玛的独特技术挑战--非正态数据处理战略

执行或推行六西格玛同志们可能有这样的感受：绿带或者黑带在服务类六西格玛项目的实施过程中遇到的最大的六西格玛技术挑战之一就是一些偏态的数据是分布的或者叫做非正态分布的数据。诚然，这个问题在制造领域也会出现，但在制造领域之外更为普遍。我们首先探讨其实质，然后提出一些符合理论并在实践中有效的对策。

在管理活动中最常遇到的连续分布是正态分布，也称为高斯分布，用于描述随机变量(如月销售额)的值的规律性。从理论上可以证明，如果一个指标受到许多随机因素的干扰或影响，并且每个干扰或影响都很小，那么所有干扰影响的综合结果将导致该指标呈正态分布。图1显示了平均值为100、标准偏差为3的正态分布。天行健咨询指出，在实际操作中，你会经常发现其他均值和标准差不同的正态分数看起来和下图差不多，唯一的区别就是曲线底部的跨度不同。

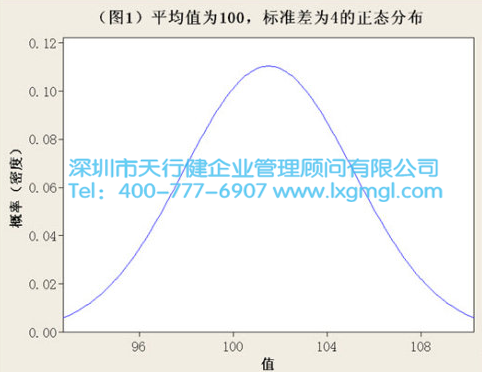
正态分布是常用统计分析工具的基础，因为大多数统计分析工具的前提是数据服从正态分布，统计分析工具有效性的关键取决于这一假设的真实性。如过程能力分析、方差分析、T检验、标准回归分析、置信区间、控制图等。实际数据不服从正态分布，我们不知道数据分布偏斜的原因。我们做什么呢

图2是人力招聘周期的数据，即从招聘需求填写时间到招聘时间的数据。这些数据与图1中的数据完全不同。它们可以被称为“右倾”，因为它们是倾斜的(不对称的)，分布高度沿横轴逐渐降低。这种数据在非制造业领域很常见。在这种情况下，数据分布趋势是倾斜的，因为不会出现负的招聘时间。

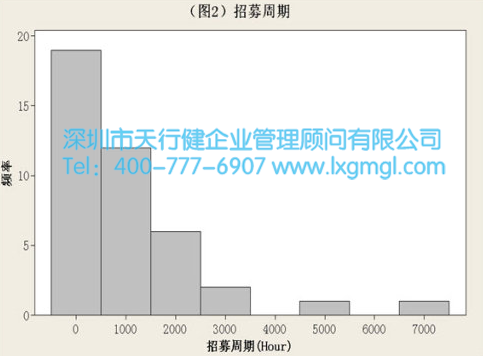
非正态数据趋势往往以其他方式出现，比如把一个从1到10的测量水平作为连续变量。在这种情况下，数据应该是离散的。因为只能得到10个独立值，所以数据不能遵循连续正态分布。

所以，如果很多统计分析工具采用正态分布，而周期测量等非制造领域的数据往往是偏态的，那是不是意味着你不能在这类情况下应用统计分析工具呢？乍一看，这是一个合理的假设，不幸的是，很多六西格玛提供商和顾问已经教过这个问题了。实际上，情况并非如此。我们可以应用标准的统计分析工具，但必须有更深入的技术理解才能决定如何应用。为了说明如何做到这一点，我们将详细介绍正态分布和正态假设，然后讨论如何分析异常数据。

要理解的最重要的原理是，正态分布是一个概念模型，即理论上存在，现实中不存在。所以，真正要回答的问题不是数据是否服从正态分布(他们不能！)，而是数据是否近似正常。说正态分布实际上并不存在可能会让人觉得奇怪，但是仔细分析正态分布就很明显了。

上面的图1显示了理论上的正态分布覆盖了从负无穷大到正无穷大，也就是说，没有最大值和最小值。所以现实中的数据如果要服从这种分布，其最大最小两端都不会有边界，这在现实中是不可能的。如果时间是一个关键的质量特性，你无法观察到负的时间，那么时间就不可能是完全正态分布，类似于金钱等等。在实践中，你永远看不到一个完整的正态分布的另一个原因是，连续分布根据定义有无限个可能的结果(数学上，为了精确定义，我们应该说“不可数无穷”)。上面的图1说明了这一点，其中分布曲线是连续的，没有中断。实际上，发生这种情况的唯一方法是，测量具有无限小数位的周期。即使你测完了，转换到小数点后两位也不能得到很多值，这样会打断分布，技术上称之为离散分布(统计学家会称之为“可数无穷”)，再次导致非正态性。

你可能会说这是一个吹毛求疵的论点，但它揭示了为什么现实中没有一个数据能完全服从正态分布，即正态分布只是一个实际意义上的概念模型。所以真实的数据并不是完全正态的，正态性是很多统计分析工具的前提。在实践中，不需要完全正态，只需要近似正态。