概率的二项分布介绍

有许多涉及在其结果有两种可能性的品质数据变量(CTQ或CTP)基础上概率分布的研究，而这两种可能性可以是发生或未发生，缺失或者完备及时或者延误。当对每一个发生或未发生的事件进行归类时，哪个结果归于发生，哪个结果归于未发生并不重要。例如，在统计过程控制的背景下，一个未能通过检测的物件可能被归于发生一类，因为过程控制的目标通常是研究非一致。在这种情况下，可以使用二项分布来分析在样本数为n时非一致物件的个数。

二项分布有四个特征，如表1所示：

表1 二项分布的特征

服务窗口处理订单的准确性是快餐店的一个重要质量性特征。每个月美食杂志都会发表其调查结果。准确性是通过由主食、副食和饮料(但遗漏了一个标准食品，如一份泡菜)组成的订单的准确完成的比例来度量的。假设在最近的一个月，麦当劳里此类订单准确完成的比例大概是90%。假设你和两个朋友去麦当劳的服务窗口，每个人要了一份刚刚提到的搭配，如果满足以下条件时，快餐订单完成情况数据会满足二项分布：

1、有一组固定数目的观察值(你朋友的3份订单)；

2、每一个观察值都被归于两类中的一类(正确的快餐订单或不正确的快餐订单)；

3、一个订单的结果与其他任何订单结果是相互独立的。

为了计算3个快餐订单里有2个准确订单的概率，参考表1得到8个可能结果，有3种方式来得到2个正确事件(本例中是两个准确的快餐订单)：

可以得出对于给定数目为n的观察，某一特定数目的事件发生(X)的概率等式。通过将得到在3个快餐订单里正确订单方式的个数(1个不正确订单)，乘以在3个快餐订单里具有某一具体顺序的两个正确订单的概率。

从以上，对3个快餐订单，有3种方式得到2个正确订单。3个订单里，以一个特定的顺序出现2个正确订单(如正确-正确-不正确)的概率是：

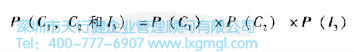
如果P=准确快餐订单的概率=0.90，那么(1-P)等于一个不准确订单的概率=0.10。那么：

3×0.081=0.243，为3个快餐订单里有两个是准确的概率。对于任何的概率值P和任何样本大小n，都可以做类似的推导。随机式(图3)展现了计算任何二项分布的一般公式。然而，随着样本空间的增大，这样的计算会变的复杂，可以使用Minitab或JMP来代替。图2为用Minitab对于快餐订单的计算。

图2  Minitab二项分布计算

图3 二项分布等式

从图2观察到零个准确快餐订单的概率是0.001, 1个准确快餐订单的概率是0.027, 2个准确快餐订单的概率是0.243，3个准确快餐订单的概率是0.729。