测量分析中四分位数的应用介绍

四分位数将样本数据分成四等份，25%的样本数据小于第一个四分位数Q1，75%的样本数据大于第一个四分位数Q1。第二个四分位数Q2:中位数，50%的样本数据大于它，50%小于它。然而，75%的样本数据小于第三个四分位数Q3，另外25%的样本数据大于Q3。

四分位数可以在等式中定义如下:

用前述的准备时间的样本的例子，将数据罗列出来：

第一个四分位数是(n+1)/4或(10+1)/4=2.75。75%的样本数据位于第二个位置的右侧。因为第二个位置的值是31，第三个位置的值是35，所以它们的差值是4。那么第一个四分位数就是34(因为31+(3/4 )× (4) = 31+3 = 34)。这意味着在25%的天数内，准备时间小于或等于34分钟。

第三个四分位数是3(n+l)/4或3(10+1)/4=8.25。25%的样本数据位于第八个位置的右侧。因为第八个位置的值是44，第九个位置的值仍然是44，所以第三个四分位数是44。这意味着在25%的天数内，准备时间大于或等于44分钟。

当数据量很大时，手工计算均值、中位数、四分位数等描述性统计量会很麻烦。此时，我们可以使用统计软件，如Minitab或JMP来帮助我们。表1显示了由Minitab计算的前一个示例中准备时间的统计数据，而图1显示了计算统计数据的JMP。表1和图1中包含的其他描述性统计数据。

表1 使用Minitab计算准备时间的描述性统计

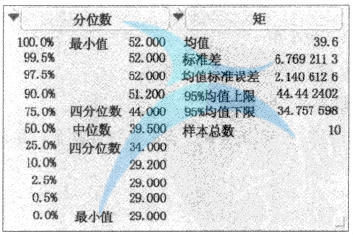
图1 使用JMP计算准备时间的描述性统计量

图2 使用JMP计算完成时间的描述性统计量

现在我们可以检查上面例子中的描述性统计。表2显示了Minitab获得的时间数据的描述性统计。图2显示了JMP的计算结果。

从表2和图2中，我们可以看到69.637和69.5这两个平均值非常接近。平均值为69.5意味着在一半的情况下，准备时间小于或等于69.5。第一个四分位数代表25%的病例，准备时间小于等于62.35。第三四分位数代表75%的病例，准备时间小于等于76.75。我们也可以知道最快完成时间是46.8分钟，最慢完成时间是101.1分钟。

表2 使用Minitab计算完成时间的描述性统计