DOE技术在起重臂优化设计中的应用

吊臂是起重机设计中最重要的部件之一，对吊臂的研究引起了广泛的关注。在以往的工程实践中，吊臂的设计多为经验设计。随着优化算法的不断完善，这类结构的优化设计成为可能。DOE(实验的设计)试验设计是一种基于概率论和数理统计的实验理论，能够科学地安排实验参数，以最少的实验次数获得准确的响应结果。

一、结构和有限元模型

本文采用的吊臂高度为8 m，宽度为7m，吊臂截面为一边长60cm的方梁结构。具体的尺寸参数如图1所示。首先利用三维软件对结构进行建模，利用Hypermesh对吊臂结构进行有限元建模。有限元模型如图2所示。

图1  

图2  

二.DOE优化流程

DOE优化过程如图3所示。优化过程大致可以描述为:根据DOE抽样理论，对结构钢板厚度的设计空间进行科学抽样。通过有限元软件二次开发的方法，将采样值嵌入有限元解文件，将解文件提交给有限元求解器，返回结构目标函数和约束响应值。根据样本点和相应的响应值，构建了优化问题的近似模型，并在此模型基础上利用优化算法进行对齐和搜索。这种方法的优点是不需要搜索原始模型。由于搜索算法的限制，很多搜索会陷入无效搜索过程，但返回原模型的响应值会浪费大量计算时间。构建优化问题的近似模型可以使优化算法在优化过程中只搜索优化后的近似模型，而不是从原模型返回响应值，使用近似模型返回响应值更快。

图3 

三.灵敏度计算

为了仔细研究吊臂的结构，将吊臂各钢板的厚度作为设计变量。每个设计变量的数量如图2所示。有10个设计变量，相当大。然而，并非所有的设计变量都对结构目标函数敏感，这可能会在后续的优化过程中浪费计算时间。因此，本文基于Plackett Burman 试验设计理论对设计空间进行采样，采样点见表1。这些样本点通过二次开发的方法嵌入到fem有限元解文件中，提交给有限元求解器，并提取它们的响应值。从每个样品返回的结构刚度、最大应力和结构质量列于表1。

表 1  

对表1中的设计变量及其响应值进行敏感性分析，分析各变量对结构刚度、最大应力和结构质量的敏感性。结果列于表2。可以得出结论，变量1的设计厚度对结构刚度、最大应力和结构质量不敏感。说明后续对这个变量的研究意义不大，所以去掉了这个变量。最后，只研究变量2-10。

表2 

第四，近似模型构建

建立近似模型有两个步骤:1 .基于Hammersley采样理论对设计变量2-10的设计空间进行采样，根据采样点通过有限元过程返回结构的响应值，拟合优化问题的近似模型；2.基于拉丁超立方体采样理论，对设计变量2-10的设计空间进行采样，并通过有限元过程返回其响应值。通过哈默斯利采样获得的采样点及其响应值列于表3。

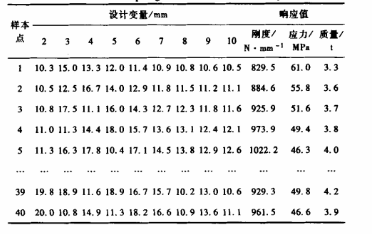
表 3  

利用拉丁超立方体对设计空间进行采样，验证拟合得到的近似模型的正确性。让近似模型返回样本点的响应值，并与表4中样本点有限元过程返回的响应值进行比较。通过对比发现，近似模型返回的响应值与有限元模型返回的响应值相对误差较小，尤其是结构质量的误差几乎为零，说明近似模型具有良好的可靠性。

表 4 

五、结构优化

遗传算法是一种模拟生物进化过程的算法。无论是线性问题还是非线性问题，都有很好的收敛性。对于给定的收敛精度，可以用较少的搜索时间满足计算要求。本文将基于遗传算法对近似模型进行优化。优化过程中，最大计算步数为200，最小搜索步数为25，种群数量为50，变异率为0.01，随机因子为1，惩罚因子为2，分布系数为5，收敛精度为0.001。结构初始刚度为1 135 N/mm，最大应力为44.3 MPa，结构质量为4.3 t，本次优化以结构刚度最大化为目标函数，约束条件为结构最大应力不超过35 MPa，结构质量不超过3.9 t。

最终优化结果是变量1-10的厚度分别为10毫米、10.01毫米、10.00毫米、10.00毫米、10.00毫米、19.96毫米、15。依次为13毫米、20.01毫米、10.87毫米和20.00毫米。优化后的结构刚度为1241.82N/mm，结构最大应力为34.82mm，结构质量为3.9t，与原结构相比，优化后的结构刚度提高了9.4%，最大应力降低了21.4%，结构质量降低了9.3%。

在本文中，借助各种DOE 试验设计理论，对设计变量进行科学采样并提交至有限元流程。通过样本点及其响应值，基于最小二乘理论拟合得到一个优化的高精度近似模型。基于遗传优化算法，对近似模型进行优化搜索。结果表明，与原结构相比，优化后的结构刚度提高了9.4%，最大应力值降低了21.4%，结构质量降低了9.3%。由于优化只研究结构钢板的厚度，对结构的拓扑和形状没有影响，加工时只需选择不同厚度的钢板即可实现。